About
GoldenPond is an experimental music notation / domain-specific programming language which adds higher level intentions or goals using the concepts from functional and modal harmony. You express music in terms of chord degrees and modifications, rather than the notes. So you can say what the music is trying to do, rather than just what it does.
The aim is to help computer based composers and live-coders, including the author, understand and apply more "advanced" music theory ideas by making them explicit and easy to express in the language.
GoldenPond was inspired by my frustration at realising that code offered so much expressivity for composing music, but that so much live-coding seemed stuck in replicating the behaviours of equipment designed for minimal loop-based music. We could describe complex chord progressions in a few keystrokes, but end up continually fiddling with a number representing the cutoff frequency of a low-pass filter. Text is a wonderfully expressive medium, but we're using it as the world's least ergonomically efficient knob!
Ultimately I'm guided by the question: "could a music programming language be expressive enough that it would be possible to live-code music of the complexity of a Mahler Symphony, on the fly?" What abstractions would such a language need? And would such a practice be viable, either technically or artistically?
GoldenPond Tutorial
The details of the GoldenPond language itself have now moved to a separate page : GoldenPond Tutorial
Try GoldenPond
In the Browser
The easiest way to play with GoldenPond is to try it now in the browser. We've taken the very nice open-source Signal Music Sequencer and retrofitted it with Goldenpond. You can try it here.
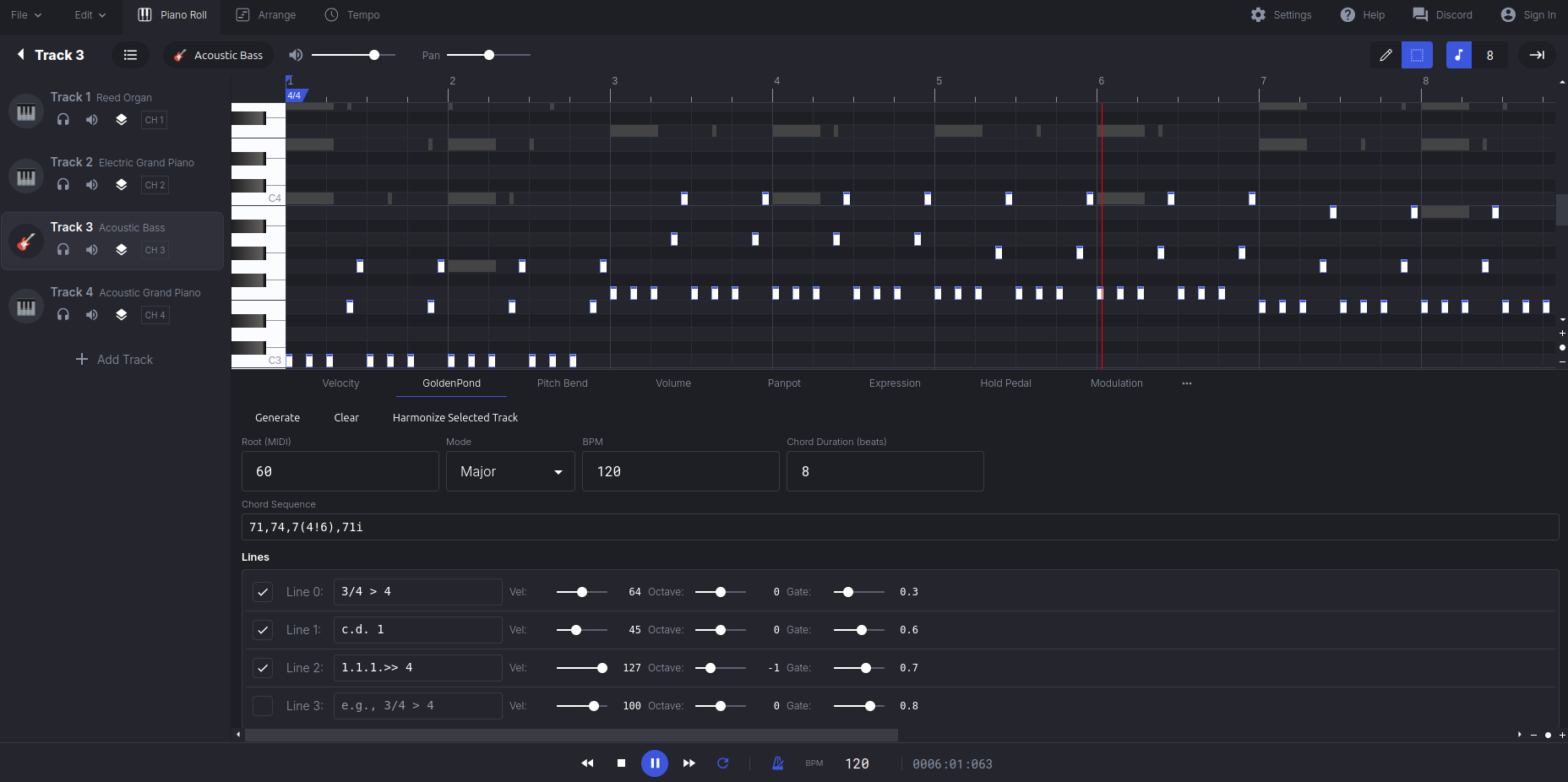
Note how a GoldenPond tab has been added to panel below the piano roll. Alongside the tabs for notewise controls on velocity, pitch bend, etc.
In the GoldenPond tab you can type the chord progression into the "Chord Sequence" box. And the various snippets of the rhythm language into the Lines boxes. This version of GoldenPond gives you 4 lines, which correspond to the first four tracks in the sequencer. Click the Generate button at the top of the panel to update the piano roll with the notes.
In FL Studio
GoldenPond is also available for FL Studio in the form of a couple of Piano Roll scripts.
There are currently two available.
- The Simple script just lets you type in a chord progression, and choose which types of Euclidean generated lines you want, and set other parameters with knobs.
- The more complex Live Coding Script gives you access to both the chord language and six parts controlled with the rhythm language. This is intended, to the extent possible within piano roll scripting, to provide Goldenpond in the form that can be used in a live-coding performance.
See instructions for installing piano roll scripts
Both scripts output each line to a separate "colour" in the piano roll so you can assign them to different instruments.
Via Python
GoldenPond is now available as a Python library on PyPI : https://pypi.org/project/goldenpond/
Github
You can also get the code on GitHub : https://github.com/interstar/golden-pond. Note that GoldenPond is now written in the Haxe programming language. From which it is transpiled to Python and Javascript. If you want to contribute to the codebase the best option is to work directly on the Haxe code. If you aren't a Haxe programmer but have made improvements directly to the Python or JS code, get in touch and we can talk about maybe moving some of your suggestions into the Haxe codebase.
Listen to GoldenPond
Experimental label, Dionysian Industrial Complex recently released an album from Mentufacturer, of experiments with GoldenPond. Each track takes a GoldenPond chord-progression, and then constructs a finished piece by adding melodies to it.